Solving systems of equations using substitution is a powerful algebraic technique, often practiced with dedicated worksheets in PDF format. These resources offer targeted practice,
building proficiency in manipulating equations and finding solutions. Mastering this method unlocks the ability to tackle complex mathematical problems efficiently.
Substitution provides a systematic approach to finding values that satisfy multiple equations simultaneously, a cornerstone of algebra and various applied fields.
What is a System of Equations?
A system of equations comprises two or more equations featuring the same variables. The goal is to find values for these variables that simultaneously satisfy all equations within the system. These systems are fundamental in algebra, representing relationships between unknown quantities. Often, practice involves solving systems of equations using methods like substitution, frequently found in worksheets available as PDF downloads.
These worksheets typically present pairs of linear equations, challenging students to determine the point where the lines represented by the equations intersect – the solution to the system. The substitution method, a key focus of these resources, involves solving one equation for one variable and then replacing that variable in the other equation. This process simplifies the problem, leading to a single equation with one variable, easily solvable. Understanding systems is crucial for modeling real-world scenarios and developing problem-solving skills.
Why Use the Substitution Method?

The substitution method offers a strategic approach to solving systems of equations, particularly when one equation is easily solved for one variable. This technique shines when isolating a variable is straightforward, simplifying the overall process. Numerous worksheets, often available as PDF files, are designed to hone this skill, providing focused practice.
Compared to other methods like elimination, substitution can be more efficient in certain scenarios. It’s especially useful when dealing with coefficients that aren’t easily manipulated for elimination. These worksheets often include problems with varying levels of difficulty, building confidence and proficiency. Mastering substitution, through consistent practice with these resources, equips students with a versatile tool for tackling a wide range of algebraic problems and real-world applications.

Understanding the Substitution Method
Substitution involves solving one equation for a variable and replacing it in the other, simplifying the system. Worksheets (PDF format) aid comprehension and practice of this core algebraic technique.
The Core Principle of Substitution
The fundamental idea behind the substitution method rests on the property that if two expressions are equal, one can replace the other without altering the equation’s truth. When dealing with a system of equations, this translates to isolating one variable in terms of the other within one equation.
Subsequently, this expression is then “substituted” into the second equation, effectively reducing the system from two equations with two unknowns to a single equation with just one unknown. This simplification allows for straightforward solving for that remaining variable.
Worksheets, often available as PDF downloads, are invaluable for mastering this principle. They provide structured practice, guiding students through the process of identifying suitable variables for isolation and accurately performing the substitution. Consistent practice with these worksheets solidifies understanding and builds confidence in applying this powerful technique.
Ultimately, the goal is to leverage the equality inherent in the system to transform a complex problem into a solvable one, and substitution is a key tool in achieving this.
Identifying Suitable Equations for Substitution
When presented with a system of equations, selecting the most appropriate equation for initial manipulation is crucial for efficient substitution. Ideally, choose an equation where one variable already has a coefficient of 1 (or -1). This simplifies the process of isolating that variable, minimizing potential errors during algebraic manipulation.
Worksheets focusing on solving systems of equations, often in PDF format, frequently present systems designed to highlight this advantage. They encourage students to scan the equations and strategically select the one offering the easiest isolation.
If no variable has a coefficient of 1, prioritize isolating the variable that appears with the smallest coefficient in any equation. This reduces the complexity of the resulting fraction when solving for that variable. Practice with diverse worksheets builds this discerning skill, leading to faster and more accurate solutions.
Remember, the goal is to set up a smooth substitution process, and careful equation selection is the first step.

Step-by-Step Guide to Solving by Substitution
Solving systems of equations via substitution, reinforced by worksheets (often PDFs), involves isolating a variable, substituting its equivalent expression, and solving for the remaining variable.
Step 1: Solve for One Variable in One Equation
Solving systems of equations by substitution begins with strategically isolating one variable within one of the given equations. This initial step aims to rewrite one equation so that it expresses one variable explicitly in terms of the other. For instance, if you encounter an equation like ‘4x + y = 6’, you might choose to solve for ‘y’, resulting in ‘y = 6 ─ 4x’.
Worksheets, frequently available as PDFs, often present systems where this isolation is straightforward – looking for coefficients of 1 is a good strategy. The goal isn’t to solve the equation entirely at this stage, but rather to rearrange it. This isolated variable will then be substituted into the other equation, effectively reducing the system to a single equation with only one variable. Careful algebraic manipulation is key, ensuring you maintain the equation’s balance throughout the process. Remember to choose the equation and variable that will simplify the subsequent steps.
This step sets the foundation for the entire substitution method.
Step 2: Substitute into the Other Equation
Having isolated a variable in Step 1, the next crucial stage in solving systems of equations by substitution involves replacing that variable in the remaining equation with the expression you derived. For example, if you found ‘y = 6 ー 4x’ and your second equation is ‘-2x ─ 3y = 7’, you would substitute ‘(6 ─ 4x)’ for ‘y’ in the second equation.
This substitution transforms the second equation into one containing only a single variable – in this case, ‘x’. Worksheets, often provided as PDFs, emphasize this careful replacement. Pay close attention to parentheses when substituting to avoid sign errors. The resulting equation can then be simplified and solved for the remaining variable. This step effectively reduces the two-equation system into a single, solvable equation, bringing you closer to finding the solution set. Accuracy in this substitution is paramount for a correct final answer.
This is the core of the substitution technique.
Step 3: Solve for the Remaining Variable
After the substitution in Step 2, you’ll be left with an equation containing only one variable. This is where standard algebraic techniques come into play to isolate and solve for that remaining variable. This might involve combining like terms, distributing, and applying inverse operations – addition, subtraction, multiplication, and division – to both sides of the equation.
Solving systems of equations using substitution relies heavily on accurate algebraic manipulation. Many worksheets, available as PDFs, provide ample practice with these skills. Remember to carefully follow the order of operations and double-check your work to avoid errors. Once you’ve determined the value of this variable, you’ve taken a significant step towards finding the solution to the entire system. This value will then be used in the next step to find the value of the other variable.
Practice makes perfect!
Step 4: Substitute Back to Find the Other Variable
With the value of one variable now known, the final step involves substituting this value back into either of the original equations. This allows you to solve for the second variable. Choosing the simpler of the original equations can streamline this process. Carefully replace the variable with its calculated value and perform the necessary arithmetic to isolate the remaining unknown.
Solving systems of equations by substitution, as practiced on numerous worksheets in PDF format, emphasizes the importance of accuracy. Double-checking your calculations is crucial. Once you’ve found the value of the second variable, you’ve successfully determined the solution to the system – an ordered pair that satisfies both original equations. Remember to verify your solution by plugging both values back into both original equations!
Verification ensures accuracy.

Examples of Solving Systems by Substitution
Solving systems of equations using substitution becomes clearer with examples, often found on worksheets in PDF format. These illustrate the process,
from simple linear systems to those with fractions or negative coefficients.
Example 1: Simple Linear System
Let’s consider a straightforward system: y = 2x + 1 and x + y = 7. Many solving systems of equations worksheets (available as PDF downloads) begin with examples like this to build foundational understanding. The key is to recognize the first equation is already solved for ‘y’.
We’ll substitute ‘2x + 1’ for ‘y’ in the second equation, resulting in x + (2x + 1) = 7. Simplifying this gives 3x + 1 = 7. Subtracting 1 from both sides yields 3x = 6, and dividing by 3 reveals x = 2.
Now, we substitute x = 2 back into either original equation. Using y = 2x + 1, we get y = 2(2) + 1, which simplifies to y = 5. Therefore, the solution to this system is x = 2 and y = 5. Worksheets often ask you to check your answer by plugging these values back into both original equations to confirm they hold true.
Example 2: System with Negative Coefficients
Let’s examine a system featuring negative coefficients: y = -3x + 5 and 2x + y = 0. Solving systems of equations practice, often found in PDF worksheets, frequently includes these to test careful manipulation of signs. Again, the first equation is already solved for ‘y’.
We substitute ‘-3x + 5’ for ‘y’ in the second equation, resulting in 2x + (-3x + 5) = 0. Simplifying gives -x + 5 = 0. Adding ‘x’ to both sides yields 5 = x, so x = 5.
Now, substitute x = 5 back into y = -3x + 5. This gives y = -3(5) + 5, which simplifies to y = -15 + 5, resulting in y = -10. Therefore, the solution is x = 5 and y = -10. Worksheets emphasize checking solutions; substitute both values into both original equations to verify their correctness, paying close attention to negative signs.
Example 3: System with Fractions
Consider a system involving fractions: x + (1/2)y = 3 and (2/3)x ─ y = 1. Solving systems of equations with fractions, a common skill tested on worksheets in PDF format, requires careful handling of the fractional coefficients. Let’s solve the first equation for x: x = 3 ー (1/2)y.
Substitute this expression for x into the second equation: (2/3)[3 ー (1/2)y] ー y = 1. Distribute the (2/3): 2 ー (1/3)y ー y = 1. Combine the y terms: 2 ─ (4/3)y = 1. Subtract 2 from both sides: -(4/3)y = -1.
Multiply both sides by -3/4 to isolate y: y = 3/4. Now, substitute y = 3/4 back into x = 3 ─ (1/2)y: x = 3 ー (1/2)(3/4) = 3 ─ 3/8 = 21/8. Thus, x = 21/8 and y = 3/4. Worksheets often require simplifying fractions as part of the solution.
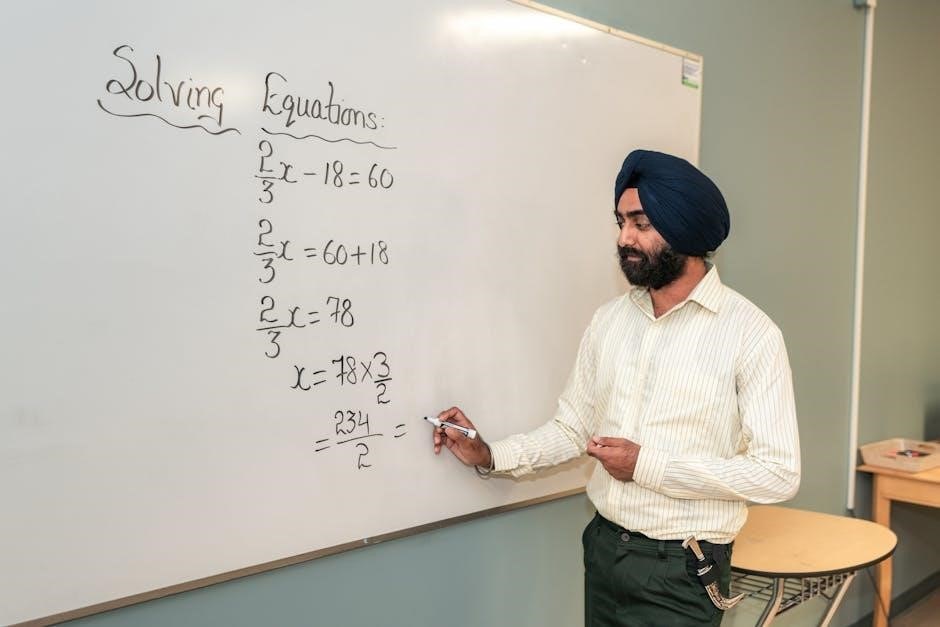
Working with Substitution Worksheets (PDF)
Solving systems of equations practice is readily available through substitution worksheets in PDF format, offering varied problems. These resources enhance skill development and reinforce concepts effectively.
Finding and Downloading Substitution Worksheets
Substitution worksheets, often available as PDF documents, are easily accessible through numerous online educational resources. A quick internet search using keywords like “solving systems of equations by substitution worksheet pdf” will yield a wealth of options from sites like Infinite Algebra, offering free trials and printable materials.
Many educational websites dedicated to mathematics provide categorized worksheets, allowing you to filter by skill level – from basic practice to more advanced problems involving negative coefficients or fractions. Teachers Pay Teachers is another excellent platform where educators share and sell their created worksheets, often including answer keys for convenient grading.
Furthermore, some school district websites and educational blogs offer downloadable PDFs directly. When downloading, ensure the source is reputable to guarantee accuracy and quality. Previewing the worksheet before downloading is also recommended to confirm it aligns with the specific learning objectives.
Types of Problems on Substitution Worksheets
Substitution worksheets, typically in PDF format, present a variety of problems designed to reinforce the method. Common exercises begin with simple linear systems where one equation is easily solved for one variable, like y = x + 1. As proficiency grows, worksheets introduce systems with negative coefficients, requiring careful attention to signs.
More challenging worksheets incorporate fractional coefficients, demanding strong algebraic manipulation skills. Some PDFs include problems where students must first rearrange an equation before substituting. Increasingly complex worksheets may present systems where substitution requires multiple steps or involves distributing to eliminate parentheses.
Beyond basic solving, some worksheets ask students to identify whether a given solution satisfies both equations in the system, or to create their own systems given specific solution sets. Word problems applying substitution to real-world scenarios are also frequently included.
Tips for Completing Substitution Worksheets
When tackling substitution worksheets (often in PDF format), prioritize careful equation rearrangement. Choose the equation easiest to solve for a single variable – look for coefficients of 1. Always double-check your substitution, ensuring the expression accurately replaces the variable in the second equation.
Pay close attention to signs, especially when dealing with negative coefficients. Distribute carefully when substituting expressions containing parentheses to avoid errors. After solving for one variable, meticulously substitute that value back into both original equations to verify your solution.
Show all your work step-by-step; this helps identify mistakes and demonstrates your understanding. If you encounter difficulty, review examples or seek assistance. Practice consistently with various PDF worksheets to build confidence and fluency.

Common Mistakes to Avoid
Substitution worksheets often reveal errors like incorrect substitution, or mistakes when solving for variables. Careful distribution and sign handling are crucial for accurate results.
Incorrect Substitution
Incorrect substitution is a frequent error encountered when working through solving systems of equations using substitution worksheets (PDF format or otherwise). Students often misplace negative signs when replacing a variable with its equivalent expression. For example, if y = 2x ─ 1, substituting into -2x ー 3y = 7 might incorrectly become -2x ー 3(2x ー 1) = 7, instead of -2x ─ 3(2x ─ 1) = 7.
Another common mistake involves substituting into the wrong equation. Remember to substitute into the equation not used to isolate the variable initially. Furthermore, ensure the entire expression representing the variable is substituted, not just a portion of it. Failing to do so leads to an unbalanced equation and an incorrect solution. Double-checking each substitution step is vital for success, and reviewing completed worksheets can highlight these recurring errors.
Carefully bracket the substituted expression to avoid distribution errors, and always verify your work!
Errors in Solving for Variables
When tackling solving systems of equations via substitution worksheets (often in PDF format), mistakes frequently occur during the algebraic manipulation of equations to isolate a variable. A common error is incorrectly applying the distributive property, leading to inaccurate expressions. For instance, when solving for ‘x’, students might mishandle coefficients or signs within parentheses.
Another frequent issue involves errors in combining like terms. Failing to correctly add or subtract terms on one side of the equation can drastically alter the solution. Additionally, dividing or multiplying both sides of an equation by a constant must be done accurately to maintain equality.
Careless arithmetic, such as simple addition or subtraction mistakes, also contributes to incorrect solutions. Always double-check each step of the variable isolation process, and utilize available resources to verify your calculations. Practicing with diverse worksheets builds confidence and reduces these errors.

Advanced Applications
Solving systems extends beyond basic worksheets; substitution tackles real-world scenarios and complex models, including three-variable systems and applied problems.
These applications demonstrate the method’s versatility.
Solving Systems with Three Variables
Solving systems containing three variables builds upon the two-variable substitution method, requiring strategic application and careful organization. Worksheets focusing on these systems, often available as PDF downloads, present a greater challenge, demanding multiple substitution steps.
The process typically involves solving one equation for one variable, then substituting that expression into the other two equations. This reduces the system to two equations with two variables, which can then be solved using familiar substitution techniques.
Once values for two variables are found, they are substituted back into any of the original equations to determine the value of the third variable. Practice with dedicated worksheets is crucial for mastering this technique, as errors in algebraic manipulation can easily occur. Look for PDF resources offering varied problem sets and step-by-step solutions to enhance understanding and build confidence.
Successfully navigating these systems demonstrates a strong grasp of algebraic principles.
Systems of Equations in Real-World Problems
Solving systems of equations isn’t merely an abstract mathematical exercise; it’s a powerful tool for modeling and solving real-world scenarios. Many worksheets, often available as PDF documents, present problems framed in practical contexts, requiring students to translate word problems into mathematical equations.
These applications range from calculating break-even points in business to determining the speeds of objects moving towards each other. The substitution method, practiced through dedicated worksheets, becomes invaluable for efficiently finding solutions to these complex problems.
PDF resources often include problems involving mixtures, distances, and financial calculations, demonstrating the versatility of this technique. Developing proficiency through practice allows students to apply algebraic skills to everyday situations, fostering a deeper understanding of mathematical concepts and their relevance. Mastering these skills builds analytical thinking and problem-solving abilities.
Real-world applications solidify the importance of algebraic proficiency.

Resources for Further Practice
Numerous online calculators and worksheet sources, including PDF downloads, offer extended practice with solving systems of equations via substitution.
These tools reinforce learning and build confidence.
Online Calculators and Solvers
Online calculators provide an immediate way to check your work when solving systems of equations by substitution, offering step-by-step solutions for verification. Websites like Symbolab and Mathway are excellent resources, allowing you to input equations and receive detailed breakdowns of the substitution process. These tools are particularly helpful when tackling more complex systems or when you’re unsure about a specific step.
Furthermore, many platforms offer the ability to generate practice problems, similar to those found on a solving systems of equations by substitution worksheet PDF. This allows for customized learning and targeted practice. Utilizing these solvers isn’t about avoiding the work, but rather about reinforcing understanding and identifying areas where further study is needed. Remember to focus on understanding the process rather than simply obtaining the answer.
Exploring these digital tools complements traditional worksheet practice, providing a dynamic and interactive learning experience.
Additional Worksheet Sources
Beyond readily available PDF worksheets, numerous online resources offer a wealth of practice problems for solving systems of equations by substitution. Websites like Kuta Software provide a vast library of free, printable algebra worksheets, including those specifically focused on this method. These often come with answer keys for self-assessment.
Teachers Pay Teachers is another excellent source, offering a variety of worksheets created by educators, often tailored to different skill levels. Khan Academy also provides interactive exercises and practice sets that reinforce the concepts. Searching for “solving systems of equations by substitution practice” will yield numerous results.
Remember to diversify your practice sources to gain a comprehensive understanding. Combining PDF worksheets with online exercises ensures a well-rounded learning experience and solidifies your mastery of the substitution technique.

